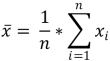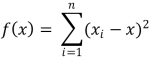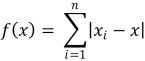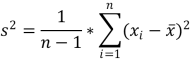Experimente

{{#seo:

|title=
|keywords=Projektarbeit Energie, projektarbeitenergie.tk, Experiment, Haushalte, Stromverbrauch, Verkleinerung, kurzfristige Energiesparmethoden
|description=Informationen zu den Experimenten von Projektarbeit Energie
|published_time=2022-05-27

}}

Es wurden zwei Experimente durchgeführt, welche die Effektivität von kurzfristigem Energiesparen herausfinden sollen. Zudem sollten diese Experimente Demoexperimente sein, um zu prüfen, wie viel Strom man in der gesamten Schweiz reduzieren könnte. Zur Prüfung unserer Thesen und um Erkenntnisse zu sammeln, standen uns zwei Haushalte bzw. zwei Familien zur Verfügung.

mathematische Statistik

Um die Daten auch richtig zu interpretieren, muss man sich mit Mathematik beschäftigen, genauer gesagt mit einem Teilbereich der Mathematik: der Statistik. Dabei erklären wir wichtige Begriffe, welche wir für die Interpretation und Auswertung der Daten unabdingbar finden. Alle Variablen haben für die Formeln die gleiche Bedeutung.

arithmetisches Mittel

Das arithmetische Mittel ist im Volksmund auch als «Durchschnitt» bekannt. Man addiert dabei alle Werte zusammen und rechnet dann durch Anzahl der Werte. Das arithmetische Mittel ist mathematisch mit dieser Formel schreibbar:

x ̅ ist die Darstellung für das arithmetische Mittel, n steht für die Anzahl Werte und x_i für einen Wert, der Datenreihe. Der Vorteil des arithmetischen Mittel ist, dass die Abstände der Quadrate der Werte zum arithmetischen Mittel minimal sind. Die Funktion hat ihren minimalen Wert:

Median

Der Median wird als Zentralwert bezeichnet und ist ähnlich wie das arithmetische Mittel. Um den Median herauszufinden, muss man zuerst alle Werte der Grösse nach sortieren. Danach wird der zentrale Wert gesucht. Wenn n ungerade ist gibt es einen mittleren Wert. Wenn n aber gerade ist, werden die zwei mittleren Werte genommen und daraus das arithmetische Mittel berechnet.

Der Vorteil des Medians ist, dass die Summe der Abstände zum Median von den Werten am kleinsten ist. Das heisst, dass sich der Median beim Minimalwert der Funktion befindet.

Standardabweichung und empirische Varianz

Ein weiteres wichtiges Werkzeug ist die Standardabweichung bzw. die empirische Varianz. Um die Streuung der Daten zu haben braucht man irgendeine Masszahl. Genau geht es um die Abweichung der einzelnen Werte vom arithmetischen Mittel:

s^2 ist die empirische Varianz, wenn man die Standartabweichung berechnen will (s) muss man nur die positive Quadratwurzel ziehen.  

Haushalt der Familie Hueber

Der erste untersuchte Haushalt war derjenige der Familie Hueber.

Informationen zum Haus(halt)

Der Haushalt besteht aus 4 Personen. Das Haus umfasst ein grosses Haus mit Garten.

Die Wahl den Haushalt der Familie Wyss für das Hauptexperiment zu verwenden, entstand als Alternative: Ursprünglich wollten wir den Haushalt der Familie Hueber nehmen. Wegen mehrerer Probleme wurde es dann aber bei der Familie Wyss gemacht. Der Hauptgrund nicht den Haushalt der Familie Hueber zu verwenden, rührte daher, dass es sich um ein altes Haus handelt mit einer alten Sicherungsinstallationen, welche vermutlich Asbest und offenliegende Leitungen beinhalten. Wir wollten keine Menschen dem Risiko eines Unfalles aussetzen oder etwas unnötig schädigen oder zerstören. Der Haushalt der Familie Wyss wird vermutlich nicht so gute Ergebnisse liefern. Das könnte hauptsächlich daherkommen, dass es sich um ein Zwei-Personen-Haushalt handelt und bereits viel auf Energieeffizienz geachtet wird. So wird z.B. seit jeher der sparende Geschirrwaschmaschinengang verwendet, Lichter werden nicht unnötig brennen gelassen oder es wird mit Restwärme gekocht. Hier bei der Messung der Familie Hueber wurde einfach schlicht vom regulären Stromzähler jeden Tag abgelesen. Jedoch waren wir trotzdem froh, das Experiment auch unter diesen Umständen durchführen zu können, auch wenn es sich bei der Familie Hueber um eine ungenauere Form des Experiments handelt.  

Ergebnisse

Da keine Messgeräte installiert werden konnten, wurde manuell jeden Abend um 21:00 der Stromzähler abgelesen und die Daten akribisch dokumentiert. Die Messungen begannen am Sonntag, dem 27. März. Um einen normalen Verbrauch zu protokolieren, wurde eine Woche der normale Stromverbrauch dokumentiert, anschliessend an diese Woche wurden alle Familienmitglieder für das Experiment geschult und mit den Massnahmen vertraut gemacht. Auf die Messung des normalen Stromverbraucht folgte eine Woche mit möglichst reduziertem Stromverbrauch. Der Fokus lag dabei vor allem beim Kochen und Backen und dem sparenden Umgang mit warmem Wasser und dem unnötigen Stromverbrauch von Elektrogeräten, welche nicht gebraucht werden, aber trotzdem Strom brauchen.

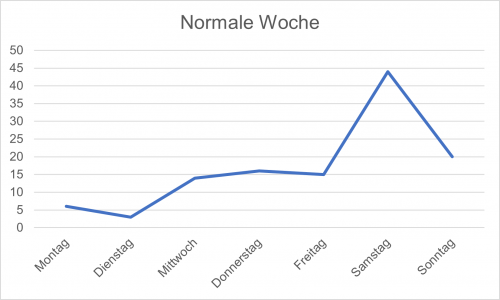
Normale Woche

Tag	Montag	Dienstag	Mittwoch	Donnerstag	Freitag	Samstag	Sonntag
kWh	6	3	14	16	15	44	20

arithmetisches Mittel	Median	empirische Varianz	Standardabweichung
16,857142857142858	15	178,14285714285714	13,347016788138731

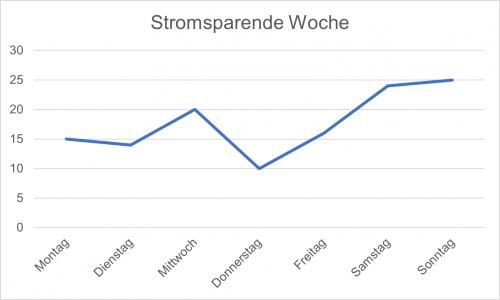
stromsparende Woche

Tag	Montag	Dienstag	Mittwoch	Donnerstag	Freitag	Samstag	Sonntag
kWh	15	14	20	10	16	24	25

arithmetisches Mittel	Median	empirische Varianz	Standardabweichung
17,714285714285715	16	30,238095238095237	5,498917642417936

Interpretation

Eine exakte Prognose, wie effektiv die Massnahmen wirklich sind, ist sehr schwer zu machen, da man dafür zwei exakt gleiche Wochen bräuchte, welche man nie haben kann. Daher kann man nur eine Schätzung abgeben, wie effektiv die Massnahmen sich auf den Stromverbrauch auswirken.

Die extrahierten Daten des Experimentes sehen verwirrend aus. Auf den ersten Blick haben wir in der stromsparenden Woche mehr Strom verbraucht, als wir in der normalen Woche gebraucht haben. Das arithmetische Mittel der normalen Woche liegt bei 16,86, dasjenige der sparenden Woche liegt bei 17,71. Der Median, der weniger empfindlich auf Extremwerte reagiert, zeigt ein ähnliches Ergebnis. Der Median der normalen Woche liegt bei 15 und der der stromsparenden Woche liegt bei 16. Beides lässt schliessen, dass wir in der stromsparenden Woche mehr Strom verbraucht haben als in der normalen Woche.

Unter der Hypothese, dass die Massnahmen im Haushalt nur eine stromsparende Wirkung haben können, muss neben den Massnahmen einen weiteren Faktor, welche sich geändert hat, eine wichtige Rolle spielen und für die Erhöhung des Stromverbrauchs in der stromsparenden Woche verantwortlich sein.

Wenn man die Standardabweichung bzw. die empirische Varianz zur Interpretation hinzuzieht, wird ein grosser Unterschied zwischen den zwei Wochen ersichtlich. Die Schwankungen der normalen Woche sind um ein Vielfaches grösser als bei der stromsparenden Woche. Dies belegt die Standartabweichung mit 13,3 in der normalen Woche und 5,5 in der stromsparenden Woche. Um die Daten richtig auszuwerten, muss man wissen, dass am Montag und Dienstag der normalen Woche sehr heisses Wetter herrschte. Dies hatte weitreichende Folgen auf den Stromverbrauch. Die Heizung war aus, alle Personen im Haushalt verbrachten viel weniger Zeit im Haus und nutzen daher auch viel weniger Elektrogeräte. Am Mittwoch änderte sich dann aber die abiotischen Umweltfaktoren in Bezug auf Temperatur und Sonne. Es wurde deutlich kälter. Diese Kälte zog sich durch das ganze restliche Experiment.

Mit dieser Schwankung der abiotischen Umweltfaktoren ist es leicht zu erklären warum man am Montag und Dienstag der normalen Woche nur insgesamt 9 kWh verbraucht wurden. Um das Experiment nicht durch diese Extremwerte zu verfälschen, fanden wir es gut sie aussenvor zu lassen.

arithmetisches Mittel	Median	empirische Varianz	Standardabweichung
51,8	16	159,2	12,617448236470002

Dies ist die Tabelle der normalen Woche exklusiv Montag und Dienstag. Wenn man die Auswertung mit diesen Ergebnissen interpretiert, ist das Ergebnis deutlich anders. Natürlich ist die Standardabweichung hingegen zu der ganzen Woche gesunken. Wenn man das arithmetische Mittel der gekürzten normalen Woche und das der stromsparenden Woche vergleicht wird ersichtlich, dass in der stromsparender Woche 18,8% weniger Strom verbraucht wurde.

Da diese Zahlen mit Vorsicht zu geniessen. Wir gehen tendenziell eher von einer Effektivität von 5 – 10% aus.

Zurück

Hauptseite

Weiter