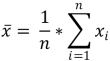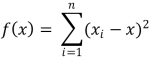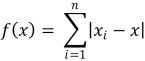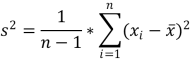Experimente

{{#seo:

|title=
|keywords=Projektarbeit Energie, projektarbeitenergie.tk, Experiment, Haushalte, Stromverbrauch, Verkleinerung, kurzfristige Energiesparmethoden
|description=Informationen zu den Experimenten von Projektarbeit Energie
|published_time=2022-05-26

}}

Es wurden zwei Experimente durchgeführt, welche die Effektivität von kurzfristigem Energiesparen belegen oder widerlegen sollten. Zudem sollten diese Experimente Demoexperimente sein, um zu prüfen, wie viel Strom in der gesamten Schweiz reduzieren könnte. Zur Prüfung unserer Thesen und um Erkenntnisse zu sammeln, standen uns zwei Haushalte bzw. zwei Familien zur Verfügung.

mathematische Statistik

Um die Daten auch richtig zu interpretieren, muss man sich mit Mathematik beschäftigen, genauer gesagt mit einem Teilbereich der Mathematik: der Statistik. Dabei erklären wir wichtige Begriffe, welche wir für die Interpretation und Auswertung der Daten unabdingbar finden. Alle Variablen haben für die Formeln die gleiche Bedeutung.

arithmetisches Mittel

Das arithmetische Mittel ist im Volksmund auch als «Durchschnitt» bekannt. Man addiert dabei alle Werte zusammen und rechnet dann durch Anzahl der Werte. Das arithmetische Mittel ist mathematisch mit dieser Formel schreibbar:

x ̅ ist die Darstellung für das arithmetische Mittel, n steht für die Anzahl Werte und x_i für einen Wert, der Datenreihe. Der Vorteil des arithmetischen Mittel ist, dass die Abstände der Quadrate der Werte zum arithmetischen Mittel minimal sind. Die Funktion hat ihren minimalen Wert:

Median

Der Median wird als Zentralwert bezeichnet und ist ähnlich wie das arithmetische Mittel. Um den Median herauszufinden, muss man zuerst alle Werte der Grösse nach sortieren. Danach wird der Zentrale Wert gesucht. Wenn n ungerade ist gibt es einen mittleren Wert. Wenn n aber gerade ist, werden die zwei mittleren Werte genommen und daraus das arithmetische Mittel berechnet.

Der Vorteil des Medians ist, dass die Summe der Abstände zum Median von den Werten am kleinsten ist. Das heisst, dass sich der Median beim Minimalwert der Funktion befindet.

Standardabweichung und empirische Varianz

Ein weiteres wichtiges Werkzeug ist die Standardabweichung bzw. die empirische Varianz. Um die Streuung der Daten zu haben braucht man irgendeine Masszahl. Genau geht es um die Abweichung der einzelnen Werte vom arithmetischen Mittel:

s^2 ist die empirische Varianz, wenn man die Standartabweichung berechnen will (s) muss man nur die positive Quadratwurzel ziehen.  

Zurück

Hauptseite

Weiter